算法核心目标

判断函数为平衡函数还是常函数 对于函数 $f: {0,1}^n \rightarrow {0,1}$

平衡函数： 由于输入总共有$2^n$种可能，那么其中一半结果是0，一半结果是1，就是平衡函数 常函数：所有结果都是一个固定值，都是0或者1

在经典计算机中，实现这样的判断至少需要两次操作， 如果是平衡函数而且运气还不错的话，两次刚好不一样，那么就是平衡函数， 如果是常函数，则至少需要$2^{n-1}+1$ 次测量

但是在量子计算中，只需要一次就能够判断。

电路实现

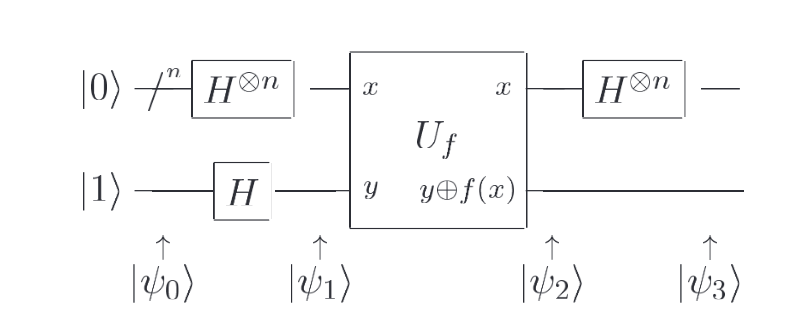
实现通用Deutsch-Jozsa算法的量子电路图如下喵 量子电路图

第一步

第一步先制备叠加态，$H^{\otimes n}$表示对于前n个量子比特都执行H门操作

此时 (|1\rangle) 就变成 (\frac{|0\rangle - |1\rangle}{\sqrt{2}})

那么 $|0\rangle^{\otimes n}$ 就会变成 $\left(\frac{|0\rangle + |1\rangle}{\sqrt{2}}\right)^{\otimes n}$

此时对于前n个量子比特都会处于一个均匀叠加的状态（描述可能不严谨），就是有$2^n$个态，包含n个比特的所有组合可能，因此可以表示成 [\sum_{x \in {0,1}^n} \frac{|x\rangle}{\sqrt{2^n}}]

所以此时的量子态可以表示为 [|\psi_1\rangle = \sum_{x \in {0,1}^n} \frac{|x\rangle}{\sqrt{2^n}} \frac{|0\rangle - |1\rangle}{\sqrt{2}}]

第二步操作

该操作相当于 $U_f : |x, y\rangle \rightarrow |x, y \oplus f(x)\rangle,$ x就是前n个量子比特 y就是初始的态 $|1\rangle$

由于 $f(x)$只可能等于0或者1

当 $f(x)=0$时 对于y的效果为 $0\oplus 0=0,1\oplus 0=1$ 你猜怎么着，没效果

如果$f(x)=1$时 就反一下呗，0变1,1变0 此时y相当于就是

[ \frac{-|0\rangle + |1\rangle}{\sqrt{2}} = -\frac{|0\rangle - |1\rangle}{\sqrt{2}} ]

提出来就相当于加了一个全局相位符号喵 - 所以f（x）的作用效果可以表示成这样

[ (-1)^{f(x)} \frac{|0\rangle - |1\rangle}{\sqrt{2}} ]

在调整一下位置，就可以知道此时

[|\psi_2\rangle = \sum_{x \in {0,1}^n} \frac{(-1)^{f(x)}|x\rangle}{\sqrt{2^n}} \frac{|0\rangle - |1\rangle}{\sqrt{2}}]

核心难理解点：我也还不理解，反正就是虽然是对于 y进行的操作，但是最终反应在 x上，y没有任何变化， 这也反应了量子计算的一个特征喵，要说原因的话就是量子纠缠吧（大概，等我补了量子力学的知识再说喵）

第三部操作

接下来就是最难而且不太好理解的部分了关于x对于任意量子态的作用可以表示为 [ H|x\rangle = \sum_z (-1)^{xz} |z\rangle / \sqrt{2} ]

其中 $x=0$或$1$，$z=0$或$1$

我带入一下看看，这个式子是否合理

x=0 的情况，此时结果应该是 $ \frac{|0\rangle + |1\rangle}{\sqrt{2}} $

带入获得

z=0的时候就是

$ |0\rangle $,

z=1的时候就是

$|1\rangle$ 结果正确喵

x=1的情况，带进入也是对的，不反复描述了

接下来让我们看看n个H门作用的结果表示

[H^{\otimes n} |x_1, \ldots, x_n\rangle =| Hx_1,Hx_2,…,Hx_n\rangle ]

都可以提取出来（物理原理保留理解，以后填充）

得到结果， [H^{\otimes n} |x_1, \ldots, x_n\rangle = \frac{\sum_{z_1, \ldots, z_n} (-1)^{x_1 z_1 + \cdots + x_n z_n} |z_1, \ldots, z_n\rangle}{\sqrt{2^n}}.] 这个可以简化成

[H^{\otimes n} |x\rangle = \frac{\sum_{z}(-1)^{x \cdot z} |z\rangle}{\sqrt{2^n}}]

即把x和z看成一个向量

x · z 是向量x与z的按位内积对2取模（不取其实也好就是奇数偶数嘛）的结果。 ${x_1 z_1 + \cdots + x_n z_n}$ 这里就可以看出来

此时

[|\psi_3\rangle = \sum_z \sum_x \frac{(-1)^{x \cdot z + f(x)} |z\rangle}{2^n} \frac{|0\rangle - |1\rangle}{\sqrt{2}}.]

见证奇迹的时刻

现在我们对于x进行测量，（为什么不对y测量，因为y没有发生改变，从第三个式子可以看出）to discern（识别） what happens

如果 $f(x)$ 是常函数，则对于全零态 $|0\rangle^{\otimes n}$ 的情况的振幅为 [\sum_x (-1)^{f(x)} / 2^n.]

由于 $f(x)$ 恒等于0或者1，所以全0态的振幅为1或者-1， 是单位长度，所以其他态的振幅一定全为0! 测量结果一定是 全0

如果 $f(x)$ 是均衡函数，此时全0态 $|0\rangle^{\otimes n}$ 的结果为0 所以测量得到的结果是至少有一个比特为1,

所以只需要测量一次就可以确定函数f到底是均衡的还是常函数

意义

直接copy 我们已经证明，量子计算机只需对函数f进行一次求值即可解决Deutsch问题，而经典计算机则需要$2^{n-1}-1$次求值。这一结果看似惊人，但存在若干重要限制条件：首先，Deutsch问题并非特别重要的问题，目前尚未发现其实际应用价值；其次，经典算法与量子算法的比较在某种程度上属于跨维度对比，因为两者对函数的求值方式存在本质差异；第三，若允许Alice使用概率性经典计算机，通过要求Bob对随机选取的若干x值进行f(x)求值，她便能以极高概率快速判定f是常数函数还是平衡函数。这种概率性场景可能比我们此前考虑的确定性场景更为现实。尽管存在这些限制条件，Deutsch-Jozsa算法仍孕育了更强大量子算法的雏形，理解其运作原理具有深刻的启示意义

就是实用性不强，但是意义重大

习题

Exercise 1.1: Probabilistic classical algorithm Suppose that the problem is not to distinguish between the constant and balanced functions with certainty, but rather, with some probability of error ε < 1/2. What is the performance of the best classical algorithm for this problem?

习题1.1：（概率型经典算法）假设问题并非以确定性区分常函数与平衡函数，而是允许存在一定错误概率（$\epsilon < 1/2$）。针对该问题的最佳经典算法性能如何？

什么时候会误判： 1.是平衡函数，但是我摸到了全0或者全1，我判断是常函数这时候错了

2.就是说摸到0和1的话就不会判断错了，只有全0全1才会导致误判

如果要满足1/2，只需要摸两次 就够了，因为全0全1都是1/4 ,加起来1/2

关于经典算法复杂度的经典知识

ai生成， 我这部分基础知识比较薄弱

记号 中文 直观含义 读法
O (Big-O) 上界 “最多只会这么慢” f ∈ O(g) 读作 “f 不高于 g”
Ω (Big-Omega) 下界 “至少会这么慢” f ∈ Ω(g) 读作 “f 不低于 g”
Θ (Big-Theta) 紧确界 “不快不慢，正好” f ∈ Θ(g) 读作 “f 与 g 同阶”
记号 在本题中的含义 具体数值  
上界 O(log(1/ε)) “随便给我一个 ε，我都能用 不超过 c·log(1/ε) 次查询搞定。”    
下界 Ω(log(1/ε)) “但你也别太贪心，任何算法都至少需要 c’·log(1/ε) 次查询。”    

（2）计算平衡函数下误判概率

（3）解出 k 的下界

要保证 ε < 1/2，必须：

[ \frac{1}{2^{k-1}} \leq \varepsilon
\Rightarrow 2^{k-1} \geq \frac{1}{\varepsilon}
\Rightarrow k - 1 \geq \log_2 \left(\frac{1}{\varepsilon}\right)
\Rightarrow k \geq \log_2 \left(\frac{1}{\varepsilon}\right) + 1 ]

因此，任何算法至少需要 k = Ω(log(1/ε)) 次查询。